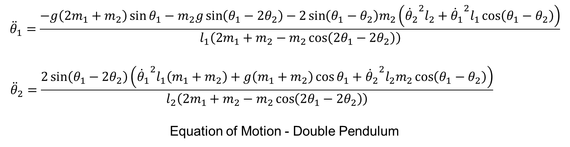Modeling & Control Systems
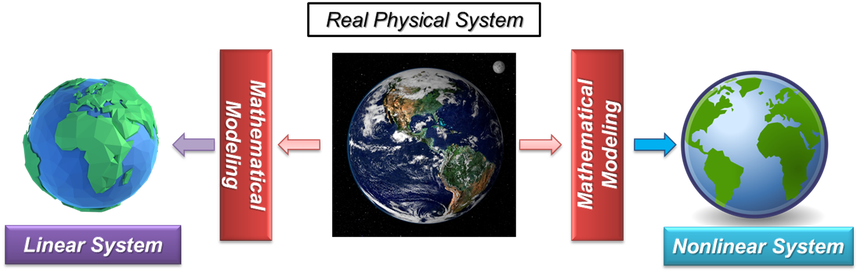
"Control systems consist of 80% system modeling and 20% controls development" - This is a common saying in the control systems community. In fact the development of a control system begins with the mathematical model of the underlying real physical system.
Often enough, the choice and methods used to model a system are consciously or unconsciously driven by the selection of the tool-set used to develop the control system. Already in the early stages of development it has to be decided whether the real physical system shall be modeled and controlled as a linear or a nonlinear system.
Often enough, the choice and methods used to model a system are consciously or unconsciously driven by the selection of the tool-set used to develop the control system. Already in the early stages of development it has to be decided whether the real physical system shall be modeled and controlled as a linear or a nonlinear system.
Linearity, Limitations & Nonlinearity
The world is inherently complex and nonlinear. Linear Systems are based on assumptions of proportionality and additivity. They are either a rare exception or at most a reasonable description of the physical relationships within a real system.
Linearity allows segregating a system into intuitive single linear subsystems and analyzes them individually before joining them back together - similar to the linear world model in the picture above.
Several well-known tools (transfer functions, Bode-analysis, PID-control, state-space-control, etc.) have been developed in order to characterize and control these systems. However this “curse of knowledge” comprises some disadvantages that significantly jeopardize control performance.
Engineers usually utilize linear tools at their disposal to comfortably model physical systems. With these methods the tracking performance, the capacity of disturbance rejection and system stability is unsatisfactory within the full working range of the system, which leads to longer development time and costs:
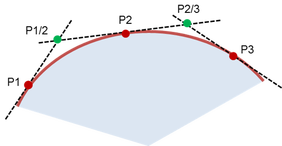
With just a straight ruler at hand, you're limited to approximate a curve by a series of tangents. This linearization involves a higher amount of work and time, since the better you want to approximate the curve, the more small tangents you need to fit onto the curve.
Linearity allows segregating a system into intuitive single linear subsystems and analyzes them individually before joining them back together - similar to the linear world model in the picture above.
Several well-known tools (transfer functions, Bode-analysis, PID-control, state-space-control, etc.) have been developed in order to characterize and control these systems. However this “curse of knowledge” comprises some disadvantages that significantly jeopardize control performance.
Engineers usually utilize linear tools at their disposal to comfortably model physical systems. With these methods the tracking performance, the capacity of disturbance rejection and system stability is unsatisfactory within the full working range of the system, which leads to longer development time and costs:
With just a straight ruler at hand, you're limited to approximate a curve by a series of tangents. This linearization involves a higher amount of work and time, since the better you want to approximate the curve, the more small tangents you need to fit onto the curve.
Though powerful, traditional linear control methods either limit the system to be operated around a single working point, or require linearization along a larger array of points, in order to guarantee overall performance. In this case the degree of linearization leads to the development of a separate controller for every single subsystem (Gain-Scheduling).
Hence following question: Wouldn't it be faster, cheaper, better performing and more convenient if there was a way to adapt the mathematical tools to the physical system instead of adapting the physical system to the mathematical tools? - Yes indeed, as shown in the "Linear vs. Nonlinear" section.
Hence following question: Wouldn't it be faster, cheaper, better performing and more convenient if there was a way to adapt the mathematical tools to the physical system instead of adapting the physical system to the mathematical tools? - Yes indeed, as shown in the "Linear vs. Nonlinear" section.
Nonlinearity is counter intuitive and sensitive to initial conditions, nevertheless these systems gained increasingly importance during the last decades: Is the dynamic behavior of two connected pendulums proportional to the dynamic of a single one? - No, the result is chaos!
Nonlinearity is a more accurate description of the relation between multiple systems and their interaction, thus its mathematical model is closer to reality but simultaneously more complex and problematic to treat. Nonlinear analysis tools gave birth to nonlinear control systems setting the starting point to a new era of innovation, that has the potential to outperform traditional linear controls methods and overcome their limitations.
Nonlinear control systems adapt to the characteristics of nonlinear physical systems and simultaneously guarantee a better tracking performance, a better disturbance rejection and a better system stability over the full working range with just a single control law. As a result this saves time and costs while increasing performance.
Nonlinear control systems adapt to the characteristics of nonlinear physical systems and simultaneously guarantee a better tracking performance, a better disturbance rejection and a better system stability over the full working range with just a single control law. As a result this saves time and costs while increasing performance.
Linear Control vs. Nonlinear Control
The choice to use nonlinear rather than linear control depends on the application, the system and the performance requirements. Linear systems and controllers are intuitive and simple, but counter intuitive nonlinear systems and controllers guarantee an overall better stability and disturbance rejection by exploiting the system's real physical properties. The “trick” lies in adapting mathematics to physics and not the other way round!
In the “Linear vs. Nonlinear” section the example illustrates the difference between the two types of controllers in terms of analytic process and calculations. The applied non-standard nonlinear controller is a SIGICONTROL development.
Test results of a real application are provided in the “Projects” section.
In the “Linear vs. Nonlinear” section the example illustrates the difference between the two types of controllers in terms of analytic process and calculations. The applied non-standard nonlinear controller is a SIGICONTROL development.
Test results of a real application are provided in the “Projects” section.