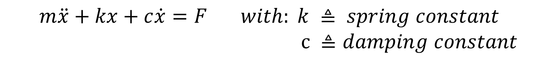Linearization
To develop a linear state-pace controller a nonlinear system has to be modeled as a linear one through its equation of motion. Therefore spring force and friction force are considered as a linear relationship between displacement and force, respectively velocity and force. Since the disturbance force is unknown and independent from the systems ‘state, it is disregarded in the linear system model; however its impact is managed with the inclusion of an integration part in the controller.
The linear equation of motion looks as follows:
The linear equation of motion looks as follows:
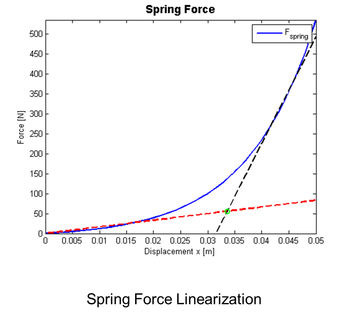
A linear model that approximates the nonlinear spring force can be the combination of two linear functions. This implies that the "k" in the equation of motion changes according to the displacement of the spring. This means that a controller gain for each of the two linear systems needs to be calculated and used dependent on the position of the mass "m". The switching position between the two controller gains is given by the intersection point of the linear functions.
(click to enlarge)
Similarly, a linear model for the friction force could be developed. As nonlinear effects occur just around the breakaway velocity (movement from standstill) it is usual to model the friction force as a damping force (with constant "c").
Implications and Limitations
As described in the "Motivation" section, the degree of linearization depends on the approximated precision required by the linear model. The more linear functions we combine to approximate the nonlinear spring force, the more sub-models and controllers need to be developed and tuned. This involves a higher investment in time and costs.
A hard switch between controller gains (Gain-Scheduling) can cause various problems, reaching from spikes in the control input and the position it is supposed to control to instability of the whole system. To avoid this undesired behavior, further preventive measures are needed in order to guarantee a smooth transition between the various control gains and to ensure control performance and stability.
An excessive deviation between the real system behavior and the modeled system can also lead to instability. This is the reason why stability limits for every sub-model need to be analyzed separately.
A hard switch between controller gains (Gain-Scheduling) can cause various problems, reaching from spikes in the control input and the position it is supposed to control to instability of the whole system. To avoid this undesired behavior, further preventive measures are needed in order to guarantee a smooth transition between the various control gains and to ensure control performance and stability.
An excessive deviation between the real system behavior and the modeled system can also lead to instability. This is the reason why stability limits for every sub-model need to be analyzed separately.
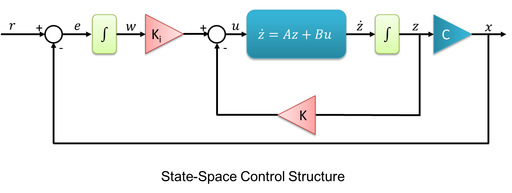
State-Space Controller
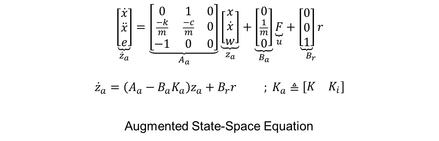
The above linear derivation allows applying the known linear control tools for state-space controllers. In this example the system description is the following:
|
Vertical Divider
(click to enlarge)
|
(click to enlarge)
|
Obviously the controller gain "Ka" has to be calculated for each single "k" used in the linearization process. This requires not only a switching mechanism between the different control gains, but also addressing the linearization offsets (offsets are proportional to the degree of linearization) due to multiple working points.
In this example the implementation of smoothing functions is left out in order to highlight the problem of a hard control gain switching for a small amount of linearization points.
In this example the implementation of smoothing functions is left out in order to highlight the problem of a hard control gain switching for a small amount of linearization points.
Control Performance
Adapting the physical model to the linear tool chain has other limits beside the switching problem. The deviation from the real spring force, the approximation of the friction force and a missing adaptation term for the unknown disturbances limit the control performance.
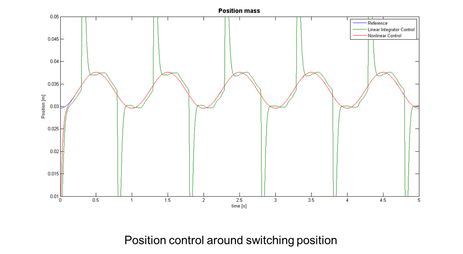
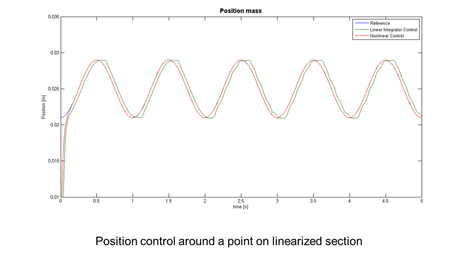
In our example we require the controller on the left picture to control the position of the mass close to the switching position, and on the right picture to control the position on a linearized section in order to avoid the switching effects. In both cases the disturbance force is inserted after a delay time of two seconds.
In our example we require the controller on the left picture to control the position of the mass close to the switching position, and on the right picture to control the position on a linearized section in order to avoid the switching effects. In both cases the disturbance force is inserted after a delay time of two seconds.
(click to enlarge)
Vertical Divider
|
(click to enlarge)
|
As predicted, in the first simulation the hard switching generates spikes in the position, hence the chosen degree of linearization and lack of smoothing measures are unsuitable for the position control. In the second simulation performance is only affected by the deviation between the modeled system and the real system. Nonlinear effects of the friction force can still be observed, in particular during changes in direction. Despite the effort of the integrator in the controller to reduce the effects of external disturbance, its influence remains visible.
In the section "Nonlinear Control", SIGICONTROL's Lyapunov-based nonlinear controller is shown to overcome this limitations.
In the section "Nonlinear Control", SIGICONTROL's Lyapunov-based nonlinear controller is shown to overcome this limitations.