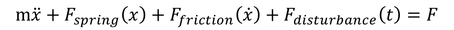Linear Control Systems vs. Nonlinear Control Systems
Linear control systems cover a large number of applications, are intuitive relatively simple. However more stringent requirements on precision, disturbance rejection and stability over the full working range are stretching the limits of this traditional technology and need further innovation.
In our daily life we do come across many systems with nonlinear behavior: Multi-link robot manipulator's mass moment of inertia, elastic properties of a muscle, traction forces of a car tire, ... .These are just few of many systems with a nonlinear behavior.
Even a simple mass-spring system has nonlinear influences that highlight the differences and limitations between the two control approaches, as shown in the following example.
In our daily life we do come across many systems with nonlinear behavior: Multi-link robot manipulator's mass moment of inertia, elastic properties of a muscle, traction forces of a car tire, ... .These are just few of many systems with a nonlinear behavior.
Even a simple mass-spring system has nonlinear influences that highlight the differences and limitations between the two control approaches, as shown in the following example.
System & Model
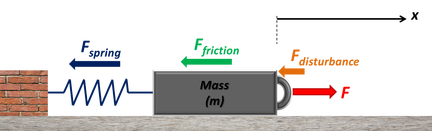
The force "F" controls the position "x" of the mass "m" connected to a spring and affected by friction and a delayed disturbance force. For this system the governing equation of motion is expressed by the following function:
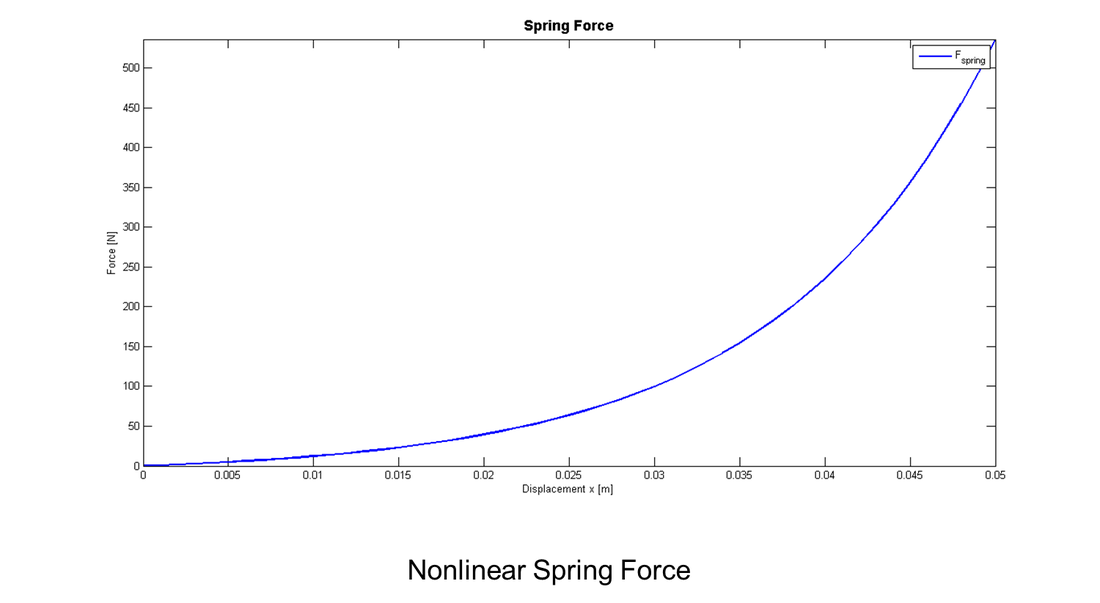
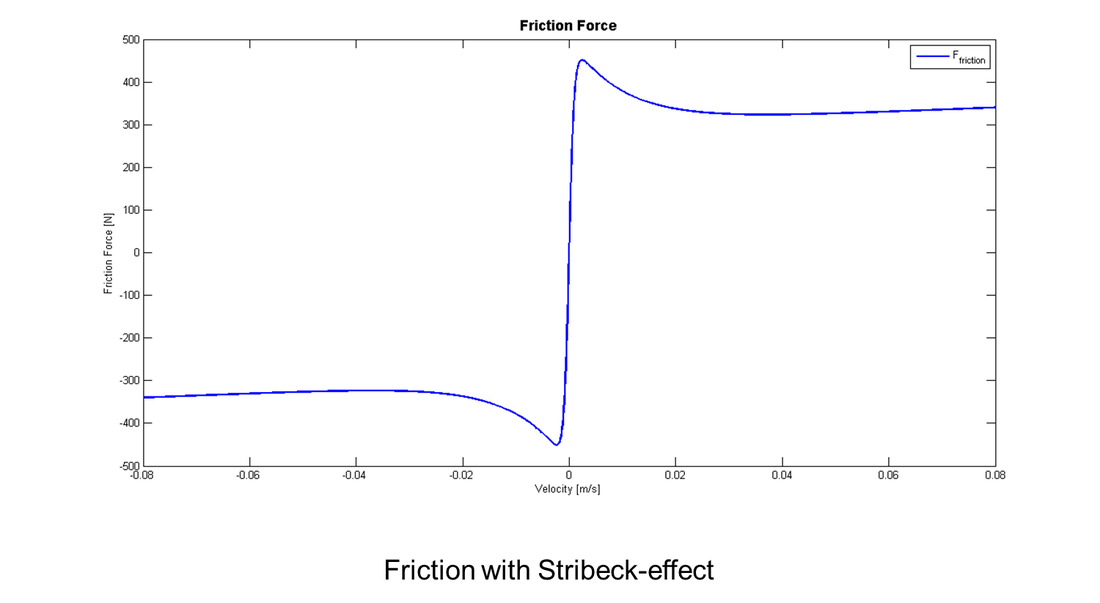
Assumptions: the spring has a nonlinear hardening characteristic, the friction force is a combination of Coulomb, static and viscous friction and the disturbance is unknown.
(click to enlarge)
|
(click to enlarge)
|
As discussed in the "Motivation" section, this is the stage for the crucial choice between a linear and a nonlinear model which will affect control performance. The developed linear state-space and nonlinear controllers are described in detail in their respective sections.
Control Performance
For a fair comparison, both controllers have been tuned to have the same step-response time and have the task of moving the mass "m" as given by the desired reference position.
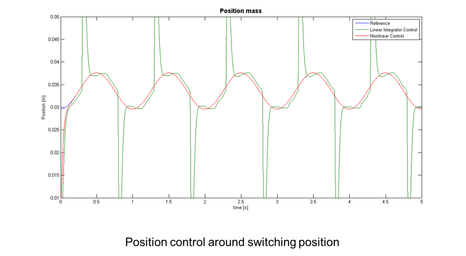
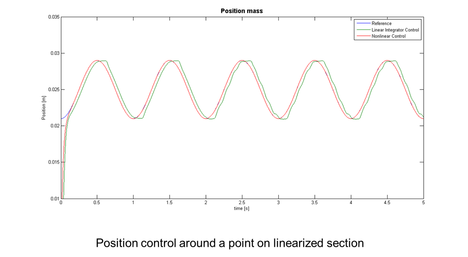
One very time consuming challenge of linear controllers on nonlinear systems is the smooth switching between the different set of control gains due to linearization. Without additional preventive measures spikes and instability in the system states can occur. In order to illustrate this particular limitation of linearization, smoothing measures in the example were left out. The difference in performance between the two control approaches is shown in the left picture for a position control close to the switching position between controller sets, in the right picture for a control within a linearized section.
One very time consuming challenge of linear controllers on nonlinear systems is the smooth switching between the different set of control gains due to linearization. Without additional preventive measures spikes and instability in the system states can occur. In order to illustrate this particular limitation of linearization, smoothing measures in the example were left out. The difference in performance between the two control approaches is shown in the left picture for a position control close to the switching position between controller sets, in the right picture for a control within a linearized section.
(click to enlarge)
Vertical Divider
|
(click to enlarge)
|
Although the linear controller is based on the precise system equations, it induces spikes in the position and is generally not able to cope with the system's nonlinearities and disturbances. With just one set of control gains SIGICONTROL's Lyapunov-based nonlinear controller is able to handle this effects and nonlinear changes in the system dynamics, improving the control performance and saving development time and costs.