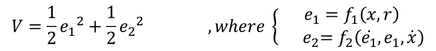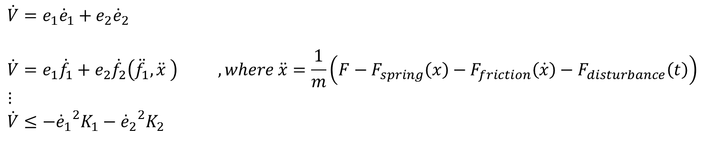Lyapunov Theorem
Nonlinear controls have become increasingly important and their research has been accelerated in the last few decades. Despite its well-researched potential, this innovation has not yet been widely diffused throughout industry.
Aleksandr Lyapunov's work "The General Problem of the Stability of Motion" (published 1892) laid out the ground for the scientific approach as follows: "A constant withdraw of energy from a system will bring the system to a state of equilibrium".
Applied to control systems this means that a control input that constantly decreases control error energy, does reduce the tracking error to zero and at the same time ensures system stability over the whole working range.
Aleksandr Lyapunov's work "The General Problem of the Stability of Motion" (published 1892) laid out the ground for the scientific approach as follows: "A constant withdraw of energy from a system will bring the system to a state of equilibrium".
Applied to control systems this means that a control input that constantly decreases control error energy, does reduce the tracking error to zero and at the same time ensures system stability over the whole working range.
Nonlinear Controller
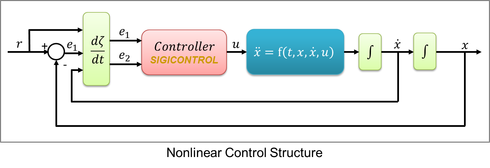
The particularity of Lyapunov-based control system lies in considering control problems from an energy point of view. In this case a real system can be modeled with a nonlinear mathematical function. This new approach simultaneously offers a solution to the nonlinear differential system equation and neither requires solving the complex equation itself nor any "Gain-Scheduling".
The most famous methods for nonlinear control designs are "Exact Model Knowledge (EMK)" and "Sliding Mode Control (SMC)". Both methods however, have their limitations in practical applications:
The most famous methods for nonlinear control designs are "Exact Model Knowledge (EMK)" and "Sliding Mode Control (SMC)". Both methods however, have their limitations in practical applications:
- EMK assumes that the system equations model the real system accurately, which by itself is a contradiction, since by definition a model is always a best guess.
- SMC has the capability to cope with system’s perturbations and disturbances that have not been included in the model, but requires the control input to act infinitely fast. No real actuator is able to meet this requirement.
Controller Development
Contrary to linear systems, nonlinear systems have no standard mathematical description but only a general function f(t,x,u). As a consequence developed nonlinear controllers can vary from application to application. Any change in the nonlinear system equation requires either another Lyapunov stability analysis or an adaption of the controller requesting a further Lyapunov stability analysis. The very specific solutions obtained with this method exploit a system’s real physical properties to achieve a desired behavior while still guaranteeing full range stability at an increased control performance.
In our example the Lyapunov candidate function, which approximately represents the error energy, looks as follows:
In our example the Lyapunov candidate function, which approximately represents the error energy, looks as follows:
For a constant energy withdrawal, the time derivative of the Lyapunov function has to be always negative. Thanks to this time derivative we can access the control input "F" in our example and have the capability to ensure that constant energy withdrawal.
Following some mathematical manipulations and correct design of the control force "F", we obtain a Lyapunov function in which as a result the time derivative is always negative, regardless of the value of the errors states. Consequently this forces the tracking error to converge to zero while ensuring system stability with just one set of control gains "Kx".
Control Performance
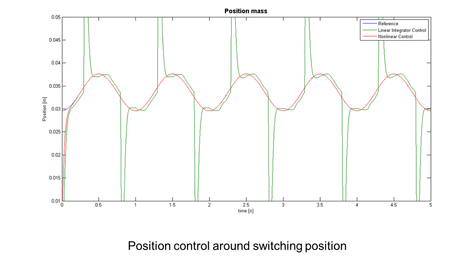
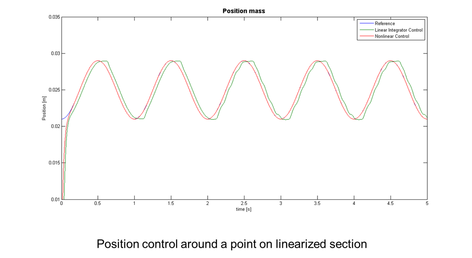
As mentioned in the "Linear vs. Nonlinear" section, the applied nonlinear controller has a better control performance than the linear one. This is the case for any desired reference trajectory. According to the comparison plots nonlinear effects in the system and the external unknown disturbances are compensated.
Since the whole working range requires just one set of control gains, the problem of switching does not exist, therefore except of the performed Lyapunov stability analysis any further stability analysis can be left out.
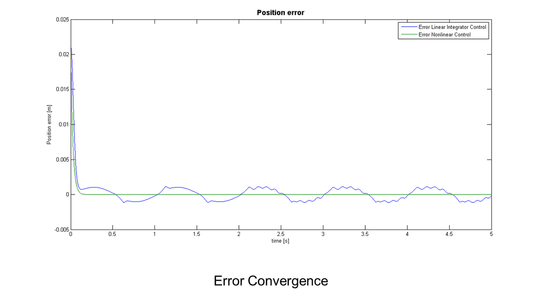
Despite the presence of unknown disturbance a closer look at the error plot confirms the asymptotic convergence to zero as predicted by the Lyapunov theorem. The plot below corresponds to a desired reference trajectory where no switching of the linear controller is triggered and compares the tracking error of the two control methods.
Despite the presence of unknown disturbance a closer look at the error plot confirms the asymptotic convergence to zero as predicted by the Lyapunov theorem. The plot below corresponds to a desired reference trajectory where no switching of the linear controller is triggered and compares the tracking error of the two control methods.